Laplace introduced the sunrise problem in 18th century. With prior knowledge that the sun has risen N days in the past consecutively (not knowing the gravity rules etc), what is your confidence that the sun will rise tomorrow?
Let p be the probability that the sun rise. Apparently p range from 0 to 1. Without any prior knowledge, we have same level of confidence to believe p=0, 0.1, 0.2, …, or 1. So we assume equal probability distribution on p.
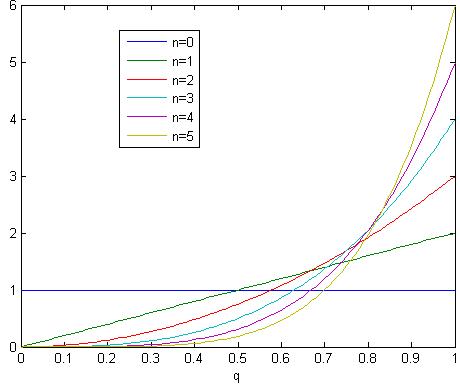
Now assume day 1 passed and we found the sun rose. Based on this knowledge, how should we update our belief on p? Well, p=0 is impossible, otherwise we will have not observed the sunrise. p=0.1 is possible but unlikely. Because if p=0.1 we only have 10% probability to observe a sunrise but we did observe one. We can actually formally calculate P(p=q|N=1) = P(N=1|p=q) * P(p=q) / P(N=1) using Bayes’s theorem. Since p(N=1) is in the denominator and it doesn’t depend on q, we don’t care. Our prior belief of P(p=q) was a uniform distribution. P(N=1|p=q) is equal to q. So the result is P(p=q|N=1) = q. After normalization (i.e. our total ‘belief’ over all p should be 1), P(p=q|N=1) = 2*q. So we have updated our belief from uniform distribution to a skewed distribution towards bigger probability of sunrise.
Based on our new belief (i.e. P(p=q)=2*q), what is our confidence that the sun will rise tomorrow? We simply need to sum (or integrate) all the possibilities. The final result equals to int(2*q^2) = 2/3. Yes, we have 2/3 confidence to say the sun will rise tomorrow, given we have observed one sunrise.
We then continue doing this for N=2, 3, …. The confidence level equals to (N+1)/(N+2). If we have observed sunrise for 1000 days, our confidence level raised to 0.999.
But if we have prior knowledge of the gravity rules, our belief will be dramatically different.
If n observations is equal to the number of days the world has existed what is the probability that the sun will rise? This with the prior knowledge of gravity, what is the probability, is it known or solvable?