The statistics toolbox in MatLab provides an easy way to do 1-way and 2-way anova. Below are some examples.
The functions are called anova1 and anovan. 1 way anova is to test if the mean in each group is same; and 2-way anova is to test (1) if the mean in each group is same, (2) if there is any interactions
1-way anova
In the first example, there is no difference between means:
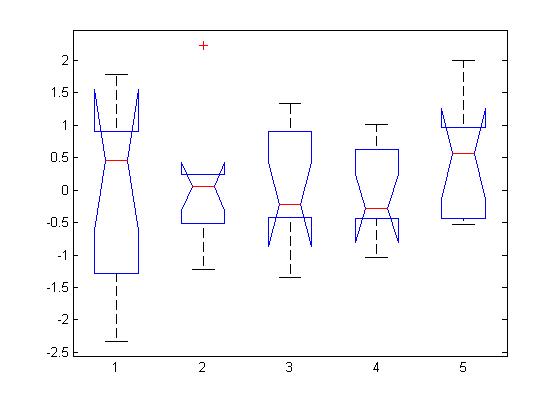
As expected, the p value is big (>0.05):
Source SS df MS F Prob>F ------------------------------------------------ Columns 1.6778 4 0.41946 0.44 0.7804 Error 43.089 45 0.95753 Total 44.7668 49
In the 2nd example, the 1st group has a larger mean
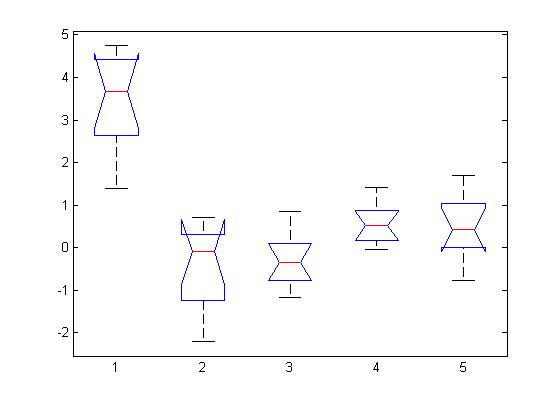
As expected, the p value is small
Source SS df MS F Prob>F ------------------------------------------------------- Columns 98.787 4 24.6969 36.94 1.10911e-013 Error 30.083 45 0.6685 Total 128.871 49
2-way anova
Let’s say we measured the height of 10 students. 5 of them are males, 5 of them has skin color ‘red’. We want to know if the height of male students is different from female students, if ‘red’ students is different from ‘blue’ students, and if the two factors have interactions (meaning the effect of gender on height is dependent on skin color).
Example 1: if the height only depends on gender, then we expect the pvalue for gender is small; p value for color or color*gender interaction is big.
Source Sum Sq. d.f. Mean Sq. F Prob>F ----------------------------------------------------------- gender 44.7625 1 44.7625 50.95 0.0004 color 0.0389 1 0.0389 0.04 0.8403 gender*color 0 1 0 0 0.9996 Error 5.2709 6 0.8785 Total 51.3893 9
Example 2: if the height depends on gender + color, then we expect the pvalue for gender and color is small; p value for color*gender interaction is big.
Source Sum Sq. d.f. Mean Sq. F Prob>F ----------------------------------------------------------- gender 67.444 1 67.4436 66.71 0.0002 color 57.215 1 57.2151 56.59 0.0003 gender*color 0.628 1 0.628 0.62 0.4606 Error 6.066 6 1.011 Total 162.43 9
Example 3: if the height depends on gender * color, then we expect the pvalue for gender and color is big; p value for color*gender interaction is small.
Source Sum Sq. d.f. Mean Sq. F Prob>F ----------------------------------------------------------- gender 0.0144 1 0.0144 0.02 0.8984 color 0.0007 1 0.0007 0 0.9768 gender*color 32.0284 1 32.0284 39.37 0.0008 Error 4.8811 6 0.8135 Total 36.9267 9
The source code:
% This is to test ANOVA in MatLab (stat toolbox)
% Xu Cui
% 2012/11/17
%% 1-way anova
% assume our data have 5 groups, and they draw from the same distribution
X = randn(10,5); % each column is a group
p = anova1(X) % As expected, p > 0.05
% assume our data have 5 groups, and the 1st group has a larger mean
X = randn(10,5);
X(:,1) = X(:,1) + 3;
p = anova1(X) % As expected, p < 0.05
% assume our data have 5 groups, and each group has a different mean
X = randn(10,5);
X = X + repmat([1:5], 10,1);
p = anova1(X) % As expected, p < 0.05
%% 2-way anova
% assume we have two factors, one is 'gender', taking values male(1) and
% female(0), the other skin color, taking value 'red' (1) and 'blue'(0). Then we
% measure the subjects' height.
gender = [ones(5,1); zeros(5,1)]; % first 5 are male
color = [1 0 1 0 1 0 1 0 1 0]';
% assume height only depends on gender
height = gender*5 + randn(10, 1) + 160;
p = anovan(height, {gender color}, 'model',2, 'varnames',{'gender';'color'})
% assume height depends on gender + color
height = gender*5 + color*5 + randn(10, 1) + 160;
p = anovan(height, {gender color}, 'model',2, 'varnames',{'gender';'color'})
% assume color and gender has interaction
height = [1 0 1 0 1 1 0 1 0 1]'*3 + randn(10, 1) + 160;
p = anovan(height, {gender color}, 'model',2, 'varnames',{'gender';'color'})
Dear Xu,
Great post, thanks. I was wandering what is with that red cross above the second group in the first figure. I searched the web with no avail 🙂 Do you happen to know what it means? It does not mean that the groups are significantly different and it appears even if one is only using first level anova.
Cheers
Interesting observation. I don’t know it either.
Xu
Hello Xu Cui and Anon, the red cross indicates an outlier, a datapoint which is further than 2 or 3 standard deviation from the group mean (depending on the way the graph is plotted, see matlab reference for details).
I can confirm Vaaal’s outlier interpretation; it seems to be a feature of Matlab’s boxplot function. It’s very useful if you are performing sanity checks on variables.
Hi all,
According to Statistics Toolbox, the plus sign at the top of the plot is an indication of an outlier in the data. This point may be the result of a data entry error, a poor measurement or a change in the system that generated the data.
By default, each outlier is a value that is more than 1.5 times the interquartile range away from the top or bottom of the box.
hi all
how can i calculate coefficient of regression model and thier significance using matlab for quadratic model
thanks