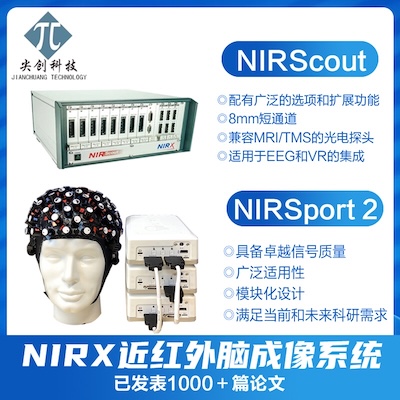
Basel problem: find the exact value of
$$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+… = ?$$
Solution:
We have by Taylor expansion:
$$\sin(x)=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+…$$
Dividing through x we have,
$$\frac{\sin(x)}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+…$$
Note, the root of \(\sin(x)/x\) is at \(n\pi\), so we can rewrite \(\sin(x)/x\) as
$$\sin(x)/x=(1-x/\pi)(1+x/\pi)(1-x/{2\pi})(1+x/{2\pi})…$$
If we multiply out the product and collect the \(x^2\) terms, we see the \(x^2\) coefficient is
$$-\frac{1}{\pi^2}(1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+…)$$
But from the original expansion of \(\sin(x)/x\), the coefficient of \(x^2\) is -1/6. These two coefficient must be equal; thus
$$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+… = \frac{\pi^2}{6}$$